LCS란?
LCS는 최장 공통 문자열(Lognest Common Substring) 또는 최장 공통 부분 수열(Longest Common Subsequence)을 의미한다. 전자는 연속된 문자열에 대한 것을 뜻하고 후자는 연속되지 않은 문자열이 포함될 수 있다.

최장 공통 문자열 (Longest Common Substring)
최장 공통 문자열을 구하는 과정은 다음과 같다.
- 문자열 A의 i번째 문자와 문자열 B의 j번째 문자를 비교한다.
- 두 문자가 같다면 ( A[i] == B[j] ) dp[i][j]에 dp[i-1][j-1] + 1을 대입한다.
- 두 문자가 다르다면 ( A[i] != B[j] ) dp[i][j]의 값을 0으로 설정한다.
- 과정중에 구한 최댓값이 최장 공통 문자열의 길이가 된다.
공통 문자열은 연속되어야 한다. 따라서 만약 현재 문자가 같다면 현재 문자까지의 공통 문자열 길이(dp[i][j])는 두 문자열의 각각 이전 문자까지의 공통 문자열 길이(dp[i-1][j-1])에 현재 문자를 더한 dp[i-1][j-1] + 1이 되는 것이다.
현재 문자가 다르다면 연속된 공통 문자열이 끝난 것이므로 dp[i][j]에 0이 설정되는 것이다.
이를 그림으로 보면 다음과 같다.

strA[1]과 strB[2]가 같은 것을 알 수 있다. 그래서 dp[1][2]는 dp[0][1] + 1이 된다.

이번에는 strA[2]와 strB[1]이 같고 strA[2]와 strB[3]이 같다. 따라서 각각 dp[2][1] = dp[1][0] + 1이 되었고 dp[2][3] = dp[1][2] + 1이 되었다.
위와 같은 과정으로 끝까지 진행하면 dp배열은 다음과 같이 채워진다.

따라서 두 문자열의 최장 공통 문자열의 길이는 2임을 알 수 있다.
최장 공통 부분수열 (Longest Common Subsequence)
최장 공통 부분수열을 구하는 과정은 다음과 같다.
- 문자열 A의 i번째 문자와 문자열 B의 j번째 문자를 비교한다.
- 두 문자가 같다면( A[i] == B[j] ) dp[i][j]에 dp[i-1][j-1] + 1을 대입한다.
- 두 문자가 다르다면( A[i] != B[j] ) dp[i][j]에 dp[i-1][j]와 dp[i][j-1]중 최댓값을 대입한다.
- dp[i][j]의 값이 두 문자열의 최장 공통 부분수열 길이가 된다.
위의 과정 중 1-1과 1-2가 왜 성립되는지를 알아보자. 먼저 dp[i][j]는 A 문자열의 i번째까지의 문자열과 B 문자열의 j번째까지의 문자열까지의 최장 공통 부분수열의 길이를 의미한다는 것을 알고 있어야 한다.
(1) 두 문자가 같을 경우 ( A[i] == B[j])
두 문자가 같을 때 dp[i][j] = dp[i-1][j-1] + 1이 된다고 했다. 공통 부분수열의 경우에는 문자열이 연속되지 않아도 되기 때문에 현재의 문자를 비교하는 과정 이전의 최대 공통 부분수열이 계속해서 유지된다. 현재 비교하는 두 문자가 같을 경우에는 두 문자를 비교하기 이전의 최댓값에 +1을 더해주는 것이다.

예를 들어 현재 strA의 인덱스가 5이고 strB의 인덱스가 3이라고 가정해보자. strA[5]와 strB[3]의 문자는 A로 같기 때문에 공통 부분수열의 길이가 +1이 될 것이다. dp[5][3]은 CAPCA와 ACA의 최장 공통 부분수열의 길이를 구하는 것인데 이는 현재 문자인 A를 비교하기 전인 CAPC와 AC의 최장 공통 부분수열의 길이에 1을 더해주면 된다.
CAPC와 AC의 최장 공통 부분수열은 AC였고 여기에 A가 추가되어 CAPCA와 ACA의 최장 공통 부분수열은 ACA가 되는 것이다.
(2) 두 문자가 다를 경우 ( A[i] != B[j] )
두 문자가 다를 때 dp[i][j] = max(dp[i-1][j], dp[i][j-1])이 된다.

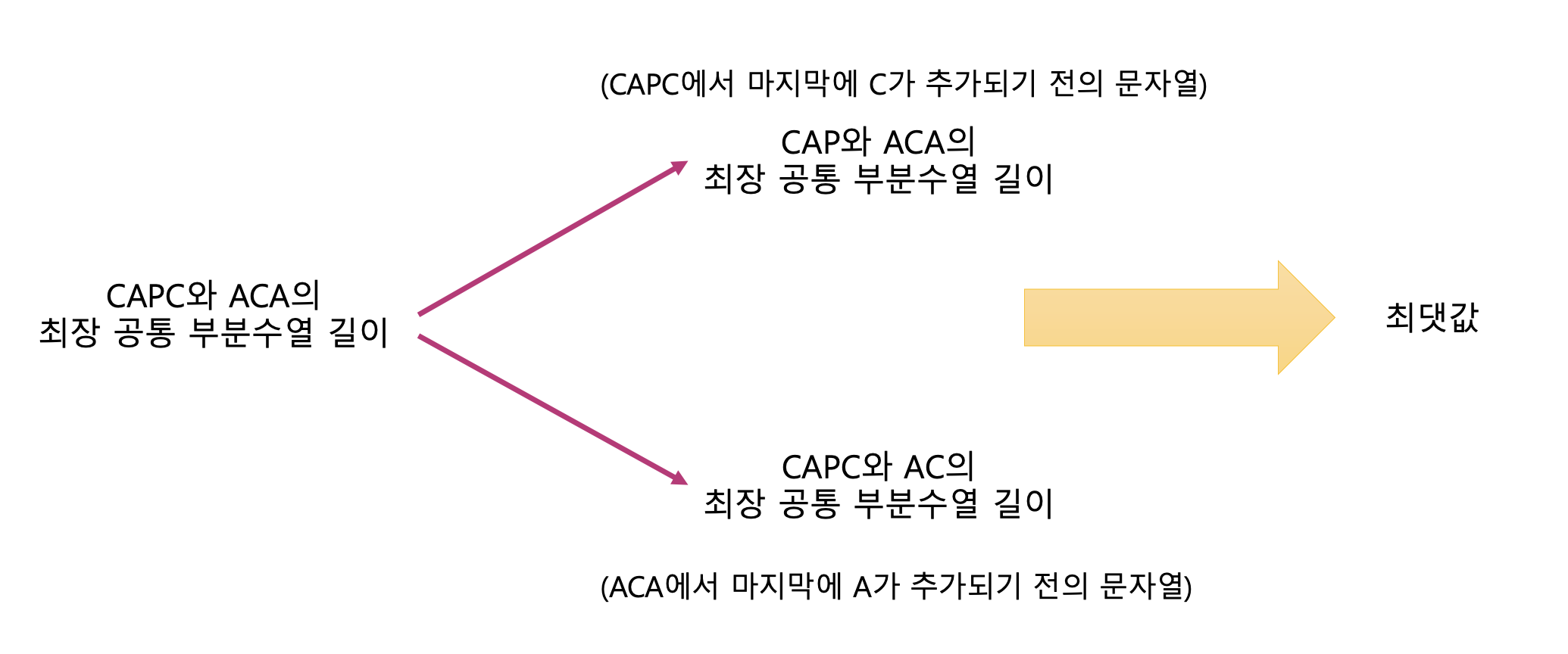
strA의 인덱스가 4이고 strB의 인덱스가 3인 경우를 보자. 이때 strA[4]는 C이고 strB[3]은 A이므로 두 문자는 다르다. 현재 CAPC와 ACA의 최장 공통 부분수열을 구해야 하나 마지막 문자는 다르기 때문에 이전에 구했던 최장 공통 부분수열의 길이를 가져와야 한다.
이를 위해 strA와 strB 각각에 마지막 문자가 추가 되기 이전에 구해두었던 최장 공통 부분수열의 길이를 찾는 것이다.
최장 공통 부분수열을 구하는 과정을 그림으로 보면 다음과 같다.
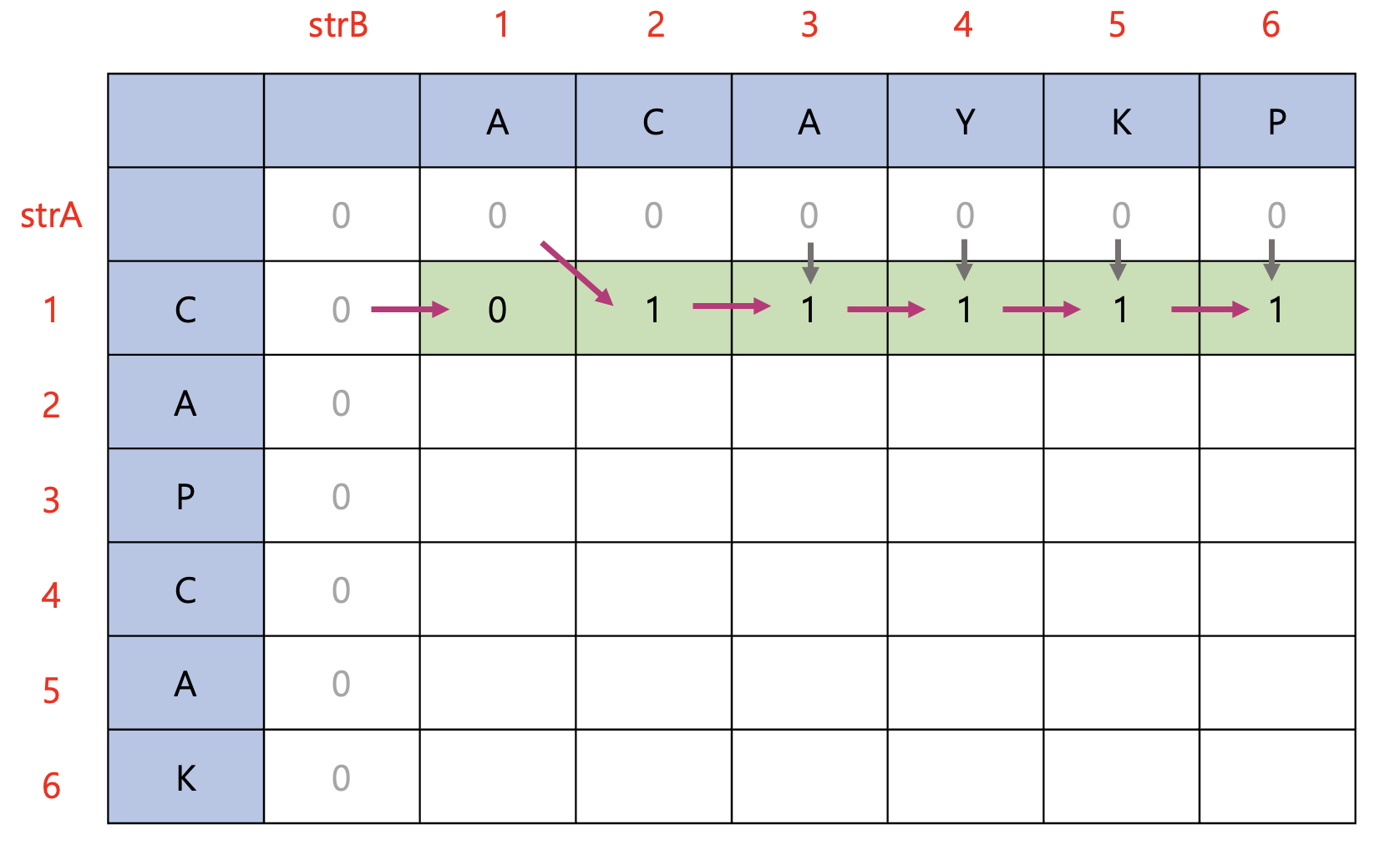
dp[1][2]는 strA[1] == strB[2]이므로 dp[0][1] + 1인 1로 설정되었다. 나머지는 두 문자열의 문자가 다르므로 dp[i-1][j]와 dp[i][j-1] 중 최댓값으로 설정되었다.
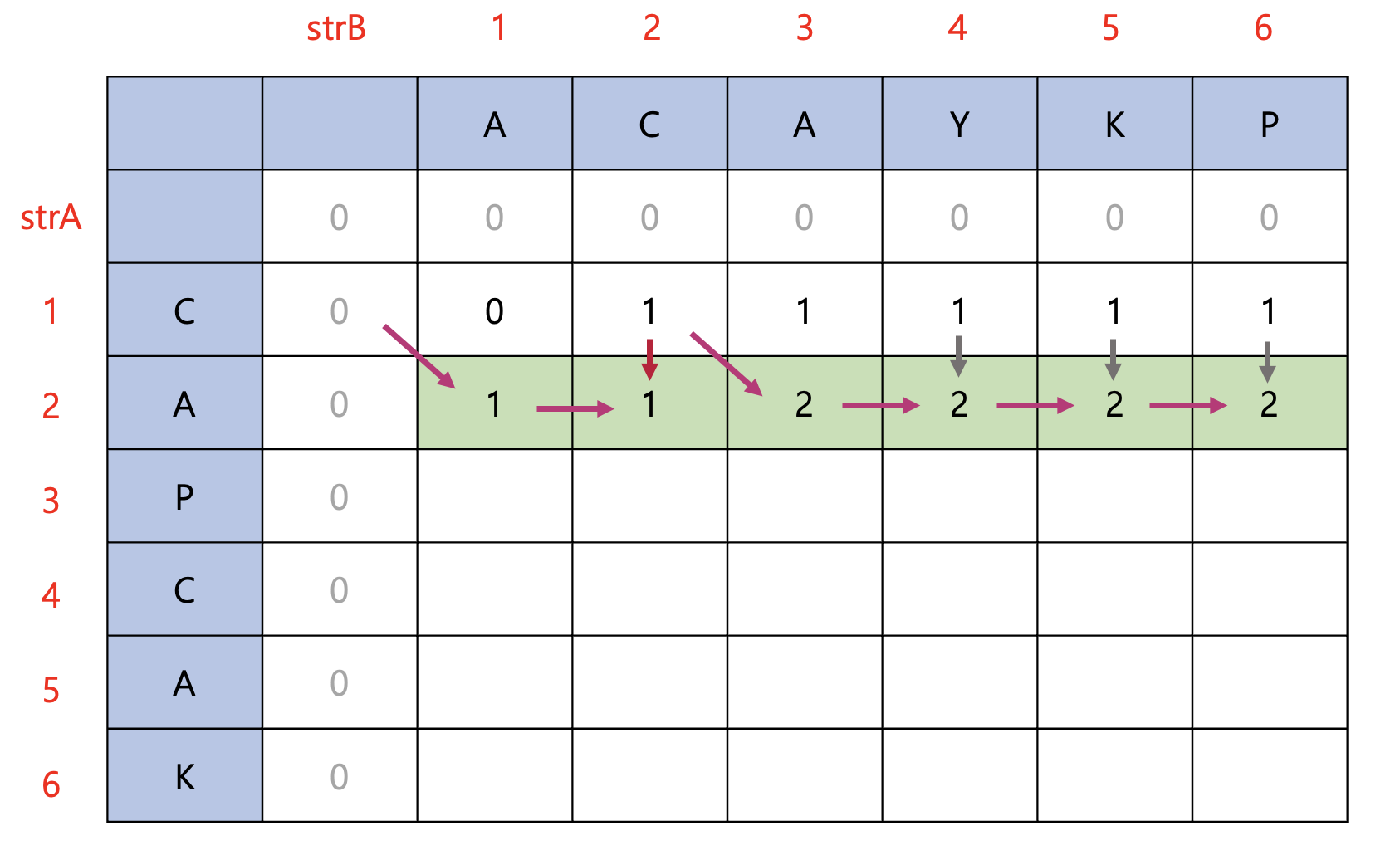
dp[2][1]과 dp[2][3]은 두 문자열의 문자가 같으므로 각각 dp[1][0]과 dp[1][2]에 +1을 해준 값으로 설정되었다.
나머지는 두 문자열의 문자가 다르므로 dp[i-1][j]과 dp[i][j-1]중 최댓값으로 설정되었다.
위와 같은 과정을 마치고나면 dp 배열은 다음과 같아진다.
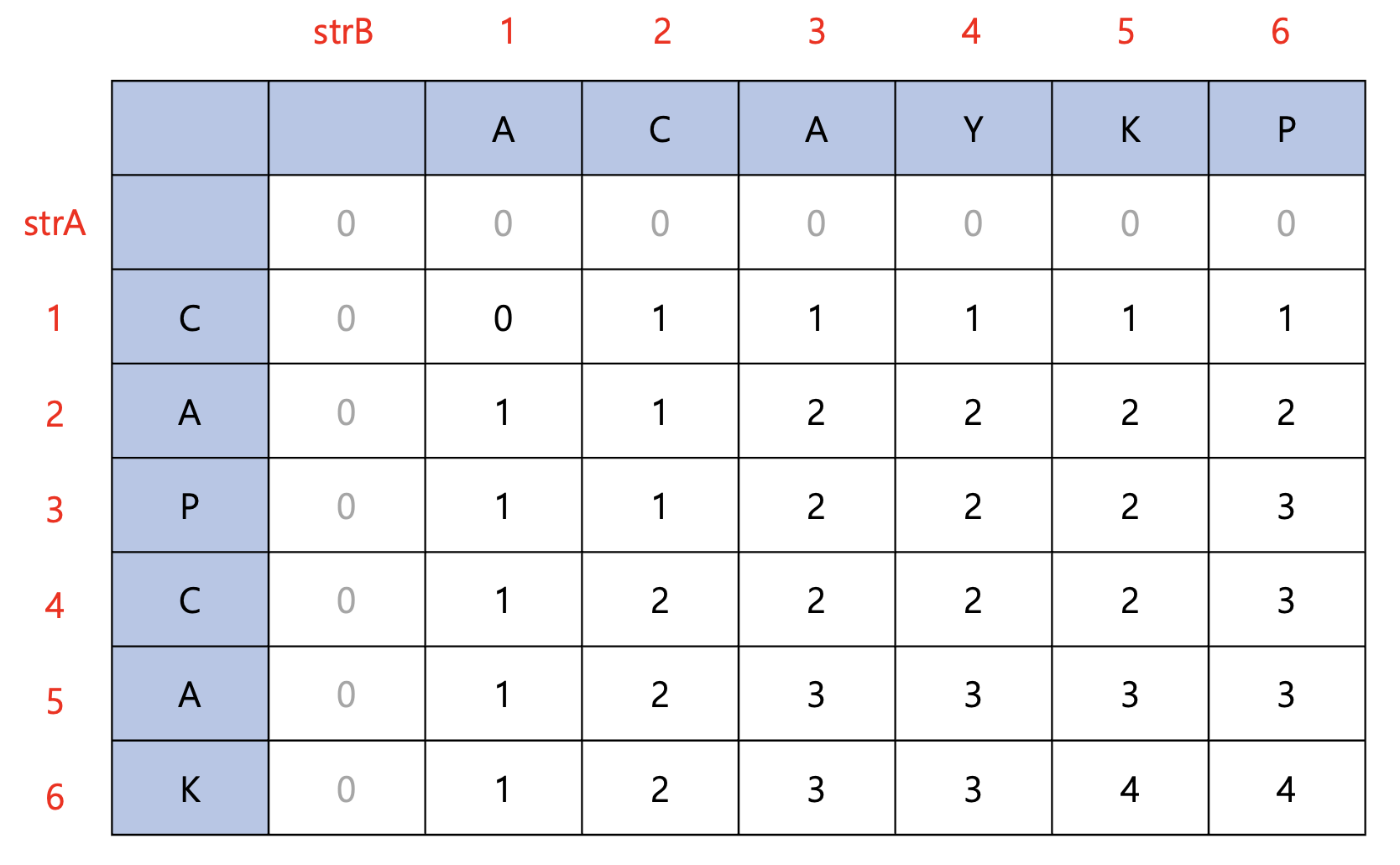
모든 과정을 끝냈을 때 dp[6][6]에 두 문자열의 최장 공통 부분수열의 길이가 들어있음을 알 수 있다.
References
'Algorithm > Basic' 카테고리의 다른 글
| [Algorithm] 세그먼트 트리 (Segment Tree) (1) | 2022.04.22 |
|---|---|
| [Algorithm] 위상 정렬 (Topology Sort) (0) | 2022.04.11 |
| [Algorithm] 최장 증가 부분 수열 (LIS) (0) | 2022.03.23 |
| [최단경로 알고리즘 - 3] 벨만 포드 알고리즘 (0) | 2021.11.14 |
| [최단경로 알고리즘 - 2] 플로이드 워셜 알고리즘 (1) | 2021.11.11 |




댓글