세그먼트 트리란?
세그먼트 트리는 완전 이진 트리를 기반으로 주어진 쿼리에 빠르게 응답하기 위해 만들어진 자료구조이다. 각 노드는 구간, 혹은 그 구간의 정보(구간합, 구간의 최솟값 등에 대한)를 저장하고 있는 자료구조이다. 리프 노드들은 길이가 1인 각각의 구간을 갖고 있고 부모 노드는 자신의 자식들의 구간의 합을 갖고 있으며 모든 구간은 연속적이다. 루트는 전체 구간을 포함하게 된다.

세그먼트 트리의 시간 복잡도 -> O(logN)
세그먼트 트리는 한 번의 연산에 O(logN)의 시간복잡도를 가진다. 만약 0번부터 7번 인덱스까지의 원소의 합을 구한다고 가정해보자. 완전탐색으로 값을 구할 경우 총 7번의 연산이 필요하다. 하지만 세그먼트 트리를 사용하면 루트 노드에 0~7까지의 구간합을 갖고 있고 따라서 단 한 번의 조회 연산으로 0~7까지의 구간합을 구할 수 있다.
N값이 굉장히 클 때 이러한 세그먼트 트리의 장점이 드러난다. N이 10e9일 경우 완전탐색의 경우 10e9번의 연산이 필요하지만 세그먼트 트리를 사용할 경우 최악의 경우 33번만에 원하는 값을 구할 수 있다. 이와 같이 세그먼트 트리를 사용하면 완전 탐색에 비해 많은 시간을 절약할 수 있다.
세그먼트 트리의 단점 -> 공간 복잡도

위의 그림은 N이 8일 때 세그먼트 트리를 구성했을 경우이다. 완전 탐색을 사용한다면 8개에 대한 메모리의 할당이 필요한데 세그먼트 트리를 구성할 경우 위 그림과 같이 총 15개 정보에 대한 메모리 할당이 필요하다.
세그먼트 트리의 구현
해당 구현은 세그먼트 트리의 노드에 해당 구간의 구간합을 저장한다고 가정한다.
(1) 세그먼트 트리 초기화 - init
# 세그먼트 트리 초기화
# start, end: 범위(구간), node: 세그먼트 트리에서 노드 번호
def init(start, end, node):
# start와 end가 같다는 것은 leaf node임을 의미한다.
if start == end:
tree[node] = nums[start]
return
mid = (start + end) // 2
init(start, mid, node*2) # 왼쪽 자식 노드의 구간합
init(mid+1, end, node*2 + 1) # 오른쪽 자식 노드의 구간합
# 왼쪽 자식 노드에 있는 구간합과 오른쪽 자식 노드에 있는 구간합을 더한 값을 저장
tree[node] = tree[node*2] + tree[node*2 + 1]1. 루트 노드(node 1)부터 시작해서 자식 노드에 대해서 재귀적으로 호출한다.
2. 리프 노드에 해당할 경우(start == end), 해당 노드에 단일 구간의 값을 넣고 return한다.
3. 왼쪽 자식 노드에 있는 구간합(tree[node*2])과 오른쪽 자식 노드에 있는 구간합(tree[node*2 + 1])을 더한 값을 현재 노드에 저장한다.
(2) 세그먼트 트리 업데이트 - update
# 세그먼트 트리 업데이트
# L: 노드의 왼쪽 구간
# R: 노드의 오른쪽 구간
# node: 현재 노드
# idx: 바꿀 값의 인덱스
# val: 바꿀 값
def update(L, R, node, idx, val):
if L == R == idx: # 단일 구간 업데이트
tree[node] = val
return
# 현재 노드의 구간에 idx가 포함되지 않을 경우
# 작업 없이 종료
if idx < L or R < idx:
return
mid = (L + R) // 2
update(L, mid, node*2, idx, val) # 왼쪽 자식 노드 업데이트
update(mid+1, R, node*2 + 1, idx, val) # 오른쪽 자식 노드 업데이트
tree[node] = tree[node*2] + tree[node*2 + 1] # 업데이트된 자식 노드들을 더해서 현재 노드의 값에 저장
만약 2번 인덱스에 있는 값을 새로운 값으로 업데이트 한다고 가정해보자. 아래 그림과 같은 순서대로 업데이트 작업이 이루어진다.



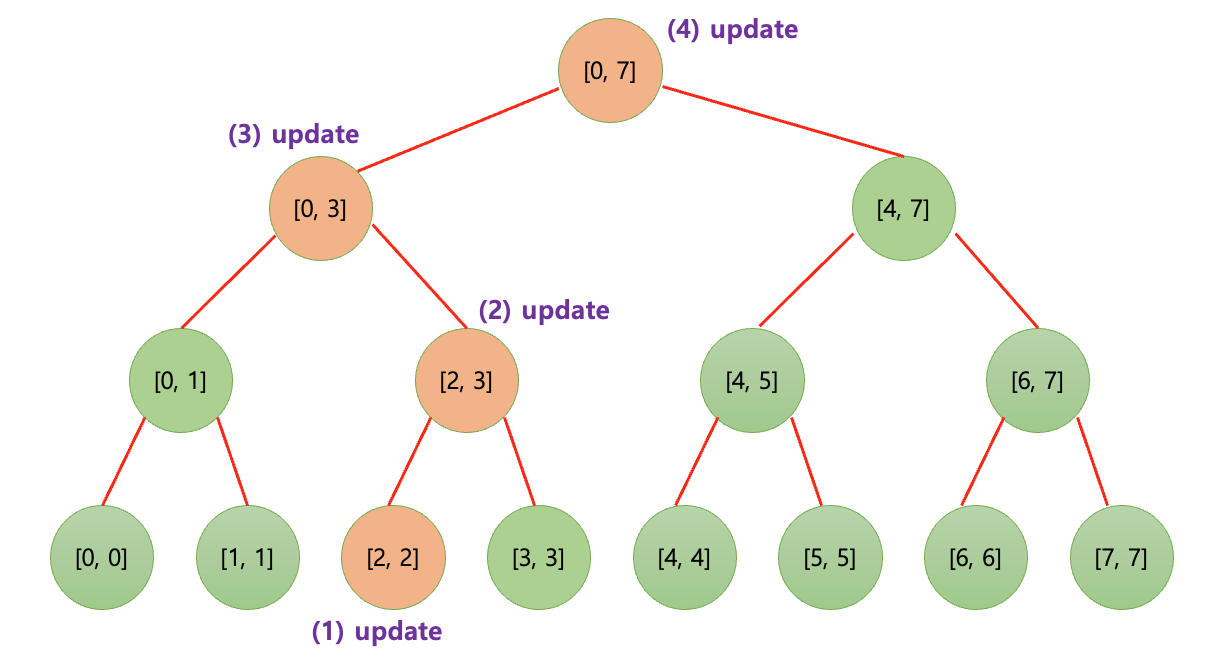
마지막에 2에 해당하는 리프 노드에 도달하고 나면 업데이트가 일어나고 리프 노드로부터 루트 노드까지 순차적으로 값이 업데이트 된다.
(3) 세그먼트 트리의 구간합 구하기 - sum
# 세그먼트 트리의 구간합
# L: 구하고자 하는 구간합의 왼쪽 구간
# R: 구하고자 하는 구간합의 오른쪽 구간
# node: 현재 노드
# nodeLeft: 노드의 왼쪽 구간
# nodeRight: 노드의 오른쪽 구간
def sum(L, R, node, nodeLeft, nodeRight):
# 구하고자 하는 구간합의 구간 안에 현재 노드의 구간이 포함되지 않는다면
# 0을 반환한다.
if R < nodeLeft or nodeRight < L:
return 0
# 구하고자 하는 구간합의 구간 안에 현재 노드의 구간이 포함된다면
# 현재 노드의 값을 반환한다.
if L <= nodeLeft and nodeRight <= R:
return tree[node]
# 구간이 겹치는 경우에는 자식 노드에 대하여 sum 함수를 호출한다.
mid = (nodeLeft + nodeRight) // 2
return sum(L, R, node*2, nodeLeft, mid) + sum(L, R, node*2 + 1, mid+1, nodeRight)
1. 원하는 구간과 노드의 구간이 만나지 않는 경우

위와 같이 노드의 구간과 원하는 구간이 일치하지 않는 경우에는 현재 노드의 값이 필요하지 않다. 구간합을 구할 때 의미 없는 구간이므로 0을 반환한다.
# 구하고자 하는 구간합의 구간 안에 현재 노드의 구간이 포함되지 않는다면
# 0을 반환한다.
if R < nodeLeft or nodeRight < L:
return 0
2. 원하는 구간에 노드의 구간이 포함되는 경우
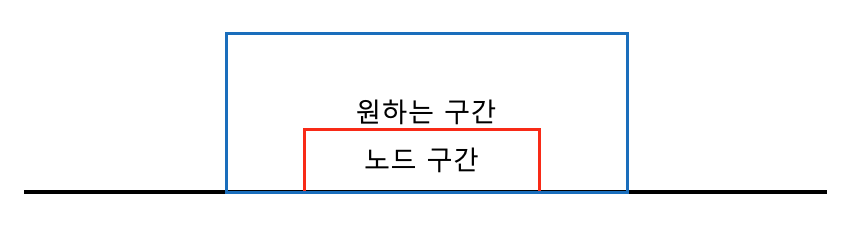
위의 그림과 같이 현재 노드의 구간이 원하는 구간안에 있을 경우 자식 노드의 값을 살펴볼 필요 없이 자신의 값을 반환하면 된다.
# 구하고자 하는 구간합의 구간 안에 현재 노드의 구간이 포함된다면
# 현재 노드의 값을 반환한다.
if L <= nodeLeft and nodeRight <= R:
return tree[node]
3. 원하는 구간와 노드의 구간이 겹칠 경우

위의 그림과 같이 구간이 겹칠 경우에는 겹치는 구간에 대한 정보가 필요하다. 겹치는 구간에 대한 값을 구하기 위해 자식 노드를 살펴 봐야 한다. 따라서 자식 노드에 대한 sum 함수를 재귀적으로 호출한다.
# 구간이 겹치는 경우에는 자식 노드에 대하여 sum 함수를 호출한다.
mid = (nodeLeft + nodeRight) // 2
return sum(L, R, node*2, nodeLeft, mid) + sum(L, R, node*2 + 1, mid+1, nodeRight)
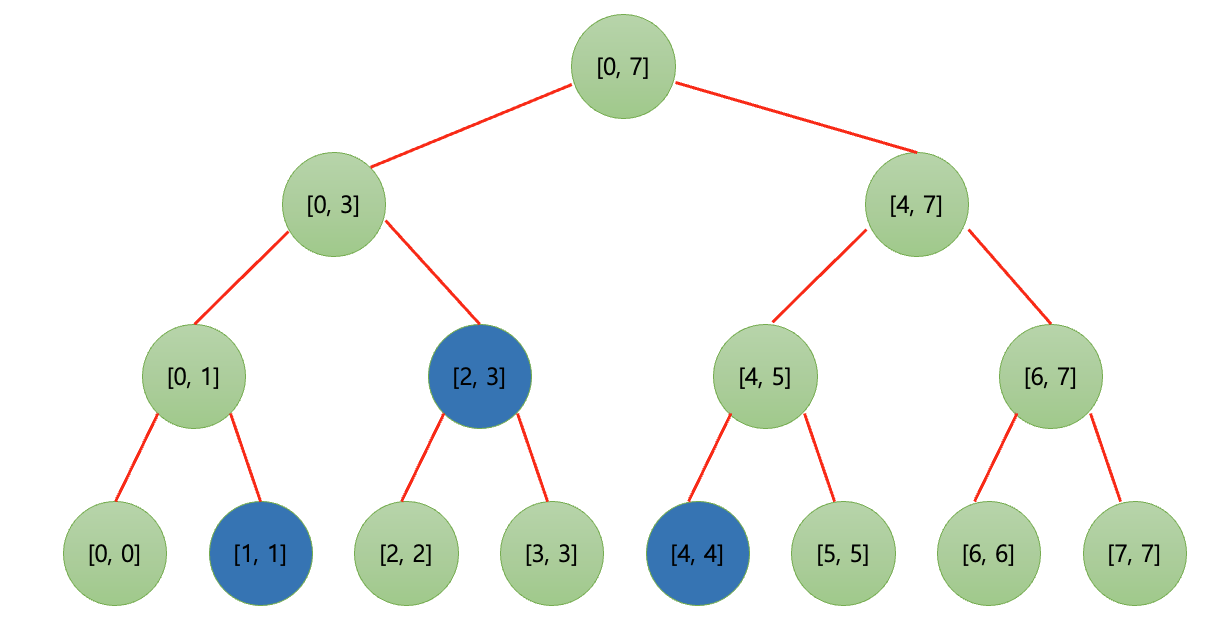
만약 [1, 4]에 대한 구간합을 알고 싶다면 세그먼트 트리에서 아래 그림에서 파란색으로 칠해진 노드에 대한 값을 가져와서 더해주면 된다.
References
- https://ojt90902.tistory.com/532
- https://blog.naver.com/kks227/220791986409
'Algorithm > Basic' 카테고리의 다른 글
| [Algorithm] LCS (Longest Common Substring / Subsequence) 알고리즘 (0) | 2022.05.01 |
|---|---|
| [Algorithm] 위상 정렬 (Topology Sort) (0) | 2022.04.11 |
| [Algorithm] 최장 증가 부분 수열 (LIS) (0) | 2022.03.23 |
| [최단경로 알고리즘 - 3] 벨만 포드 알고리즘 (0) | 2021.11.14 |
| [최단경로 알고리즘 - 2] 플로이드 워셜 알고리즘 (1) | 2021.11.11 |




댓글